Exponents
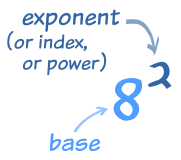
The exponentof a number says how many times to use the number in a multiplication.
In 82 the "2" says to use 8 twice in a multiplication,
so 82 = 8 × 8 = 64
In words: 82 could be called "8 to the power 2" or "8 to the second power", or simply "8 squared"
Exponents are also called Powers or Indices.
Some more examples:
Example: 53 = 5 × 5 × 5 = 125
- In words: 53 could be called "5 to the third power", "5 to the power 3" or simply "5 cubed"
Example: 24 = 2 × 2 × 2 × 2 = 16
- In words: 24 could be called "2 to the fourth power" or "2 to the power 4" or simply "2 to the 4th"
Exponents make it easier to write and use many multiplications
Example: 96 is easier to write and read than 9 × 9 × 9 × 9 × 9 × 9
You can multiply any number by itselfas many times as you want using exponents.
Try here:
In General
So in general:
an tells you to multiplya by itself,
so there are n of thosea's: |
|
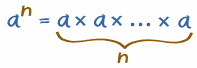 |
Other Way of Writing It
Sometimes people use the ^ symbol (above the 6 on your keyboard), as it is easy to type.
Example: 2^4 is the same as 24
Negative Exponents
Negative? What could be the opposite of multiplying?
Dividing!
A negative exponent means how many times to divide one by the number.
Example: 8-1 = 1 ÷ 8 = 0.125
You can have many divides:
Example: 5-3 = 1 ÷ 5 ÷ 5 ÷ 5 = 0.008
But that can be done an easier way:
5-3 could also be calculated like:
1 ÷ (5 × 5 × 5) = 1/53 = 1/125 = 0.008
In General
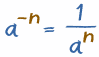 |
That last example showed an easier way to handle negative exponents:
- Calculate the positive exponent (an)
- Then take theReciprocal (i.e. 1/an)
|
More Examples:
| Negative Exponent |
|
Reciprocal of Positive Exponent |
|
Answer |
| 4-2 |
= |
1 / 42 |
= |
1/16 = 0.0625 |
| 10-3 |
= |
1 / 103 |
= |
1/1,000 = 0.001 |
| (-2)-3 |
= |
1 / (-2)3 |
= |
1/(-8) = -0.125 |
What if the Exponent is 1, or 0?
| 1 |
|
If the exponent is 1, then you just have the number itself (example 91 =9) |
| |
|
|
| 0 |
|
If the exponent is 0, then you get 1(example 90 = 1) |
| |
|
|
| |
|
But what about 00 ? It could be either 1 or 0, and so people say it is"indeterminate". |
It All Makes Sense
My favourite method is to start with "1" and then multiply or divide as many times as the exponent says, then you will get the right answer, for example:
| Example: Powers of 5 |
| |
.. etc.. |
|
 |
| 52 |
1 × 5 × 5 |
25 |
| 51 |
1 × 5 |
5 |
| 50 |
1 |
1 |
| 5-1 |
1 ÷ 5 |
0.2 |
| 5-2 |
1 ÷ 5 ÷ 5 |
0.04 |
| |
.. etc.. |
|
If you look at that table, you will see that positive, zero or negative exponents are really part of the same (fairly simple) pattern.
Be Careful About Grouping
To avoid confusion, use parentheses () in cases like this:
| With () : |
(-2)2 = (-2) × (-2) = 4 |
| Without () : |
-22 = -(22) = - (2 × 2) = -4 |
| With () : |
(ab)2 = ab × ab |
| Without () : |
ab2 = a × (b)2 = a × b × b |